Das analoge Schließen
Auf dieser Seite finden sich
Informationen zum analogen Schließen, dem in der
kognitiven Psychologie große Bedeutung zugemessen
wird. Diskutiert werden Analogien beim Problemlösen,
die klassische Analogien, die eine wichtige Rolle beim
logischen Denken und der Entscheidungsfindung (deduktives
Schließen, modus ponens, modus tollens,
Schließen mit Quantoren, induktives Schließen,
Bayes-Theorem, Monte-Carlo-Effekt, subjektiver Nutzen,
subjektive Wahrscheinlichkeit) spielen. Die deduktive Logik
umfaßt die Fälle in denen Schlüsse mit
Gewißheit gefolgert werden können.
Was ist analoges Schließen?
Dem analogen Denken wird in der kognitiven Psychologie große Bedeutung zugemessen, da es in den verschiedensten Bereichen eine zentrale Rolle spielt, z.B. für das Lernen an Beispielen, für effektives Problemlösen und kreatives Denken; nicht zuletzt werden wichtige wissenschaftliche Entdeckungen zurückgeführt auf "Denken in Analogien".
Analogie (griech. Übereinstimmung) bedeutet das Verhältnis von Gleichartigkeit oder Ähnlichkeit zwischen zwei oder mehreren Dingen. So wird z. B. oft die Analogie bzw. Ähnlichkeit zwischen dem menschlichen Herzen und einer mechanischen Pumpe hervorgehoben. In derLogik bezeichnet man als Analogie eine induktive Form der Beweisführung. Wenn zwei oder mehrere Größen in einer oder mehreren Hinsichten einander ähnlich sind, besteht die Möglichkeit, dass sie auch in anderen Hinsichten einander ähnlich sind. Wenn sich z. B. ein Schüler in der Schule meist erfolgreich zu Wort meldet, daraufhin bei den Aufnahmeprüfungen für die Universität sehr gute Ergebnisse erzielt und schließlich ein überdurchschnittlich guter Student wird, so wird ein zweiter Schüler bei gleichem Verhalten in der Schule an der Universität voraussichtlich auch ein hervorragender Student sein.
Zwei Bereiche lassen sich unterscheiden:
Analogien beim Problemlösen:
Hier geht es darum, inwieweit das Lösen eines Problems dadurch erleichtert werden kann, dass auf die Lösung eines anderen Problems, das ein analoges Prinzip enthält, Bezug genommen wird.
Beispiele für analoge Zuordnungen:
Die Lösung der Bestrahlungsaufgabe von Duncker, bei der ein inoperabler Tumor im Körperinneren nur durch die Zentrierung schwacher Strahlen abgetötet werden kann, soll erleichtert werden durch die Analogie zur Belagerungsaufgabe, bei der Truppen verteilt aufmarschieren, um vermintes Gelände zu überwinden.
In einem anderen Beispiel erfahren Kinder wie ein Magier mit Zauberkräften seinen Teppich zu einer Röhre zusammenrollt, um Edelsteine durchgleiten zu lassen; in der nachfolgend zu lösenden Aufgabe geht es dann - diesem Prinzip entsprechend - darum, einen Bogen Papier zu einer Röhre zusammenzurollen, um darin Bälle in ein nicht direkt erreichbares Gefäß zu befördern.
Klassische Analogien:
Die klassische Analogie ist - zurückgehend auf Aristoteles - definiert als Gleichheit der Relation von vier Termen/Begriffen (A, B, C, D), wobei der zweite (B) mit dem ersten (A) in der gleichen Beziehung steht wie der vierte (D) mit dem dritten (C).
Abgekürzt dargestellt A:B = C:D.
Mit solchen Analogie-Aufgaben, z.B. dunkel:hell = naß:trocken, wird in psychometrischen Verfahren die Fähigkeit des analogen Schließens als wichtige Teilkomponente der Intelligenz erfaßt.
Siehe auch zum Schließen aus psychologischer Sicht:
Die entwicklungspsychologische Frage, ab welchem Zeitpunkt Kinder analoges Schließen beherrschen, wird zum einen aus Ergebnissen psychometrischer Forschung beantwortet; sie zeigen, dass viele Kinder noch im Alter von 11-12 Jahren einfache Analogien nicht "richtig" bilden können und häufig assoziative Verknüpfungen bzw. Ergänzungen vornehmen.
Diese Befunde entsprechen auch der Theorie
Piagets, die analoges Denken als sich erst spät
entwickelnde Fähigkeit annimmt und der Stufe des
formal-operatorischen Denkens (ca. ab dem 12. Lebensjahr)
zuweist.
Diese Annahme stützt Piaget auf die Unterscheidung von zwei Arten von Relationen, die den Stufen der konkreten und formalen Operationenrzugeordnet sind:
1. Relationen erster (niedrigerer) Ordnung betreffen - voneinander unabhängig - nur die Beziehung zwischen den jeweiligen Vergleichspaaren A: B bzw. C: D. Die Relationen werden sukzessiv verarbeitet.
2. Relationen zweiter (höherer) Ordnung verbinden die Beziehungen erster Ordnung in dem Sinne, dass sie auf Gleichheit/Ähnlichkeit der Beziehung zwischen den Paaren abzielen ("relationale Ähnlichkeit").
Logisches Denken und Entscheidungsfindung
Deduktives Schließen, Modus ponens, Modus tollens
Die deduktive Logik umfaßt die Fälle in denen Schlüsse mit Gewißheit gefolgert werden können. Etwa in Fällen von bedingten bzw. konditionalen Aussagen, wie z.B. "Wenn ich viel Bier trinke, dann bin ich betrunken". Konditionale Aussagen bestehen aus dem Antecedens ("wenn"-Teil) und dem Konsequens ("dann"-Teil). Bei streng logischer Betrachtung gibt es zwei Schlußfolgerungen, die aus einer konditionalen Aussage ("Wenn A, dann B") gefolgert werden können:
|
|
i) |
Wenn A gilt, dann gilt B (Modus ponens) |
|
|
ii) |
Wenn B nicht gilt, dann gilt A nicht (Modus tollens) |
In Versuchsreihen wird oft mit konditionalen Syllogismen gearbeitet, einer Kombination aus einer konditionalen Aussage, einer Prämisse und einer Schlußfolgerung. Die Testpersonen müssen nun entscheiden, ob sich wirklich die Schlußfolgerung aus der Prämisse und der Aussage folgern läßt. Dabei wurde der Modus ponens in den allermeisten Fällen korrekterweise als richtig erkannt, während nur die wenigsten den Modus tollens als richtig akzeptieren.
Weitere oft gemachte Fehleinschätzungen sind die Ablehnung des Antecedens ("Wenn A, dann B", A gilt nicht -> B gilt nicht) und die Bestätigung des Konsequens (B gilt -> A gilt). Eine mögliche Erklärung für die beiden zuletzt genannten Fehleinschätzungen wäre, dass die Testpersonen die Aussagen als bikonditional interpretieren. Aber nur die Erklärung, dass Menschen nicht streng logisch sondern probabilistisch schließen, erklärt auch die starke Ablehnung des Modus tollens. Kann die Aussage aber erlaubnisbezogen interpretiert werden, liefern die Testpersonen logisch korrektere Ergebnisse.
Schließen mit Quantoren, Atmosphärenhypothese
Auch bei kategorialen Syllogismen, bestehend aus zwei Prämissen und einer Conclusio, werden häufig falsche Conclusiones akzeptiert. Ein unzureichender Erklärungsversuch ist die Atmosphärenhypothese: Conclusiones, die ähnliche Ausdrücke wie ihre Prämissen aufweisen, werden als richtig betrachtet.
Eine bessere Erklärung liefert die Theorie der mentalen Modelle: Der Mensch konstruiert sich ein mentales Modell und prüft auf die Korrektheit der Conclusio. Ebenfalls würde eine probabilistische Sicht der Prämissen das Verhalten der Testpersonen sehr gut erklären.
Induktives Schließen, Bayes-Theorem, Monte-Carlo-Effekt
Das induktive Schließen umfaßt die Fälle, in denen Schlüsse nur mit einer gewissen Wahrscheinlichkeit gezogen werden können. Mit Hilfe des Bayes-Theorems kann aus der a-priori Wahrscheinlichkeit p(A) und den bedingten Wahrscheinlichkeiten p(B|A) und p(B|¬A) die a-posteriori Wahrscheinlichkeit p(A|B) ermittelt werden.
Menschen unter- bzw. überschätzen jedoch häufig die Wahrscheinlichkeiten, weil sie die kumulative Kraft von eingetretenen Ereignissen unterschätzen. Das tatsächliche Verhalten stimmt aber mit dem Bayes-Theorem überein ("implizite Übereinstimmung"). Eine der weiteren häufig auftretenden Fehleinschätzungen bei der Benennung von Wahrscheinlichkeiten, wäre z.B. der Monte-Carlo-Effekt: Viele Testpersonen sind so etwa der Meinung, dass bei dem Werfen einer Münze nach einer Reihe von gleichen Seiten, das Fallen der anderen Seite wahrscheinlicher sein müße, als wieder dieselbe Seite zu erhalten.
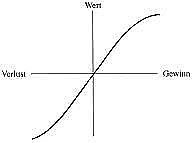
Subjektiver Nutzen
Bei einem Gewinnspiel um Geld ist der subjektive Nutzen des Geldes nicht gleich dem Nennwert. Der Verlustbereich verläuft steiler als der Gewinnbereich.
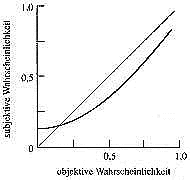
Subjektive Wahrscheinlichkeit
Sehr kleine Wahrscheinlichkeiten werden gegenüber großen Wahrscheinlichkeiten überbewertet.
Produktives Denken und schöpferischer Problemlösungsprozess
Karl Duncker, der bis zur Auflösung des Psychologischen Institutes im Jahr 1935 Schüler und Mitarbeiter der Begründer der Gestaltpsychologie der Berliner Schule, Max Wertheimer, Wolfgang Köhler und Kurt Koffka, veröffentliche bedeutende Arbeiten zum produktiven Denken und zu schöpferischen Problemlösungsprozessen. Karl Duncker wurde 1903 in Leipzig geboren. Die Nazis verboten ihm die Habilitation, weil sein Vater Kommunist war. Deshalb emigrierte er 1935 in die USA. Dort starb er 1940 im Alter von nur 37 Jahren. Duncker war einer der bedeutendsten Vertreter der Gestalttheorie. Er veröffentliche des Weiteren bedeutende Arbeiten zur Kritik des Behaviorismus, zur Phänomenologie der Gefühle und Empfindungen und zur Psychologie der Ethik. 1934 fand er im Exil in England, in Cambridge bei Frederic Charles Bartlett eine Anstellung und wurde dann von Wolfgang Köhler an das Swarthmore College in Pennsylvania berufen. Aus seinem 1935 in Berlin erschienenen Buch "Zur Psychologie des produktiven Denkens" stammt folgendes Rätsel:
"Eines Tages begann Moses bei Sonnenaufgang auf den Berg Sinai zu steigen. Er ging unterwegs mal schnell und mal langsam und machte in unregelmäßigen Abständen Pausen. Bei Sonnenuntergang erreichte er den Gipfel. Am nächsten Morgen bei Sonnenaufgang begann er den Abstieg. Er nahm denselben Weg wie beim Aufstieg, ging wieder völlig unregelmäßig und machte häufig Pausen. Bei Sonnenuntergang erreichte er den Fuß des Berges. Kann es sein, dass Moses auf dem Rückweg zu einer bestimmten Uhrzeit an einem Ort war, wo er zur genau gleichen Uhrzeit auch am Vortag war?" --> Die Lösung!
Psychologische Theorien zur Erklärung des analogen Schließens
Strukturalistische
Position
Modell
derInformationsverarbeitung
Wissensbasierter
Ansatz
Quellen
Luchins, A. S. (1942). Mechanization in Problem Solving. In: Psychological Monographs 54 (S. 248).
Duncker, Karl (1935). Zur Psychologie des produktiven Denkens. Berlin: Springer.
Popper, Karl R. (1979). The Bucket and the Searchlight: Two Theories of Knowledge. In Objective Knowledge: An Evolutionary Approach (rev. ed.). Oxford: Clarendon Press.
Oerter, Rolf & Dreher, Michael (1995): Entwicklung
des Problemlösens. In Oerter, Rolf & Montada, Leo
(Hrsg.), Entwicklungspsychologie. Weinheim: PVU.
Schütz, Tassilo (2000). Problemlösen und
Entscheidungsfindung.
WWW:
http://www.informatik.tu-muenchen.de/~schuetz/psycho/paper/paper.htm
(01-01-06)
Riegler, Alexander (1999). Können wir das Problem der
Echtzeitkognition lösen?
WWW: http://www.zum-thema.st/wissensbank/Riegler1.html
(02-05-18)
inhalt :::: nachricht :::: news :::: impressum :::: datenschutz :::: autor :::: copyright :::: zitieren ::::