Konkret-operatorisches Denken

Die Strukturen oder Operationssysteme dieser Phase ermöglichen nun die Bewältigung der zuvor erwähnten Schwierigkeiten. Diese Operationssysteme stellen einen wichtigen Teil der geistigen Werkzeuge des Menschen dar. Später in der formal-operatorischen Phase werden sie nicht ersetzt, sondern ergänzt durch einige noch komplexere Systeme.

In der konkret-operationalen Phase sind die Kinder fähig, die Ordnung nach einer Dimension (z.B. Länge), die sog. Seriation asymmetrischer Relationen, vorzunehmen, die das verhältnismässige Korrelat des Ordnens im Sinne einer Aufreihung nach einer Dimension (z.B. Grösse) beinhaltet. Die Entwicklung des Seriationsverhaltens versuchte Piaget anhand einer Aufgabe darzustellen, bei der die Grössenverhältnisse dreier unterschiedlich langer Stäbe angegeben werden mussten. Die Kinder müssen über die Erkenntnis der Transitivität verfügen.

Zunächst wird also der grössere Stab A neben Stab B gezeigt. Danach wird der grössere Stab B neben Stab C gezeigt. Nun wird das Kind gefragt, welcher Stab nun länger sei, A oder C. In der konkret-operationalen Phase ist die Lösung solch logischer Probleme, die auf einer Inklusionsbeziehung beruhen, möglich. Das Denken hat also sozusagen über die Wahrnehmung gesiegt.

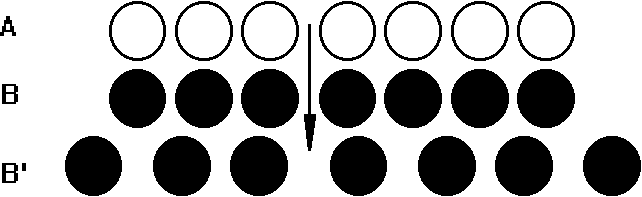
Der Zahlbegriff setzt die Invarianz der Anzahl bei Veränderung der Anordnung voraus. Einem Kind werden zwei Reihen mit gleich vielen Chips gezeigt, dabei wird aber die eine Reihe in die Länge gezogen. Dies führt bei jüngeren Kindern zur Behauptung, dass diese Reihe nun mehr Chips enthalte, weil sie länger ist, oder weniger, weil die Lücken grösser sind. Das Aufsagenkönnen der Zahlenreihe vermittelt also dem Kind in dieser Phase noch keine für die Einsicht in die Invarianz nützliche Information. Ein fünfjähriges Kind kann zwar die Chips beider Reihen zählen und zur gleichen Anzahl gelangen, dies führt aber trotzdem nicht zur Einsicht in die mengenmässige Gleichheit der beiden Reihen. Die verwendeten Zahlworte haben im Sinne des Zahlbegriffs noch keine operatorische Bedeutung. Gemäss Piaget ist der Zahlbegriff erst möglich, wenn das Kind über die Fähigkeit verfügt, alle Objekte abzuzählen, was voraussetzt, dass alle Objekte als gleiche Einheiten behandelt werden (z.B. Chips). Dies ist eine der Leistungen der Klassenbildung. Doch wenn abgezählt wird, muss das Kind noch über eine Ordnungsrelation verfügen: zunächst das erste, dann das zweite, dann das dritte Element, usw.. Piaget verweist auf eine Struktur, die in dieser Weise eine Ordnung von Elementen erlaubt, nämlich die asymmetrische Relationsbildung: a<b<c<d...

Reihenbildung

 

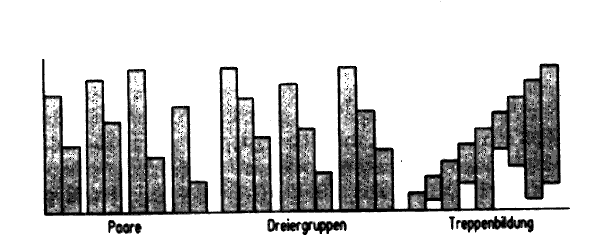
Abb.: Fälle unvollständiger Reihenbildung

 

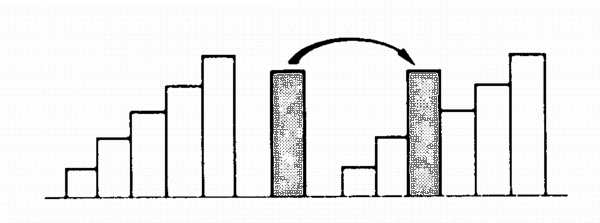
Abb.: Fehler bei der Einordnung eines Elements in eine bestehende Reihe

 

Seriation asymmetrischer Relationen

 

Abb.: Prüfanordnung zur Erfassung der Einsicht in die Zahlenkostanz