Formal-operatorisches
Stadium
Formal-operatorisches
Stadium
Das formal-operatorische Denken geht in spezifischer Weise über vorgefundene oder vorgegebene Informationen hinaus. In dieser Phase wird nicht mehr nur aufgrund der aktuell gegebenen Informationen gefolgert und geurteilt, sondern es werden mögliche weitere Informationen einbezogen, die man zu gewinnen sucht.
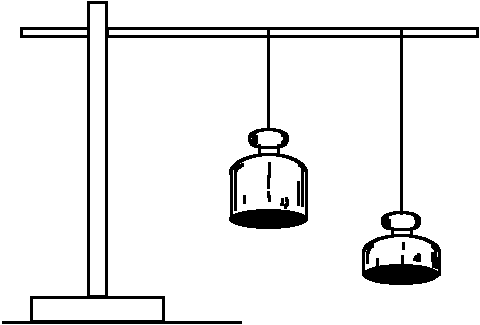
Pendelversuch
Abb.: Pendelversuch zur Ermittlung des Stadiums der geistigen Entwicklung, nach Piaget, in Oerter/Montada S. 440
- Kinder in der präoperationalen Phase neigen dazu, nur eine der beiden Dimensionen zu beachten: Sie werden sagen, ein kurzes Pendel schwinge schneller, oder aber sie behaupten, ein schweres Pendel schwinge schneller. Dies ist ganz davon abhängig, welches der beiden in der Demonstration kombinierten Merkmale sie gerade ins Auge fassen.
- Kinder in der konkret-operationalen Phase sind bereits in der Lage, mehrere Merkmale zu kombinieren und werden sagen, ein kurzes und schweres Pendel schwinge schneller (was ja auch beobachtbar ist). Es leistet also eine logische Konjunktion beider Dimensionen, was aber in diesem Falle nicht zur Lösung des Problems führt, da das Gewicht des Pendels nicht relevant ist.
- Kinder, die sich bereits in der formal-operationalen Phase befinden, lösen sich von diesen konkret beobachteten Fällen (kurz/schwer und lang/leicht) und sehen diese als zwei von vier möglichen Kombinationen der beiden Variablen Gewicht und Länge, wenn diese je zwei Werte aufweisen. Sie wollen auch die noch nicht realisierten Kombinationen der beiden Dimensionen empirisch überprüfen, sie wollen also auch noch ein langes/schweres Pendel und ein kurzes/leichtes Pendel beobachten. Die neue Leistung besteht darin, dass sie ihren Schlussfolgerungen eine systematische Kombination von Variablen zugrundelegen, aus den gedachten Kombinationsmöglichkeiten Hypothesen ableiten und diese prüfen. Die Variablen werden also kontrolliert und isoliert, man bedient sich mental einer 4-Felder-Tafel.
Dadurch ist ein erstes zentrales Merkmal des formal-operatorischen Denkens umschrieben. Das Kind fixiert sich nicht mehr bloss auf gegebene Informationen. Es abstrahiert aus Beobachtungen und Aussagen mögliche Einflussvariablen, erstellt ein System möglicher Kombinationen solcher Einflussvariablen, das prinzipiell vollständig überprüft werden muss, bevor die richtige Lösung gefunden werden kann.
Zum Proportionalen Denken gestaltete Piaget einen Versuch, bei dem den Kindern zwei leere Gefässe gezeigt werden: A und B. Nun werden einige Becher mit Flüssigkeiten in jedes der Gefässe gegossen. Einige dieser Becher enthalten Orangensaft, andere enthalten Wasser. Das Kind soll nun voraussagen, welches der beiden Gefässe schliesslich eine Mischung aus Orangensaft und Wasser enthalten wird, die stärker nach Orangensaft schmeckt. Das Kind kann die Zahl der Becher zählen, die in jedes Gefäss gegossen werden sollen, aber es darf die Becher nicht wirklich in das Gefäss giessen und probieren. Folgende Sequenz von Lösungsstrategien wurden beobachtet:
- Strategie 1 (3 bis 4 1/2 Jahre): diese besteht aus einem isolierten Zentrieren. Das Kind beurteilt jede Reihe mit Bechern für sich, ohne Vergleich. Es registriert lediglich, ob ein Becher mit Saft dabei ist oder nicht. Es löst daher nur jene Probleme, in denen nur auf einer Seite ein Glas mit Saft steht, es versagt aber in allen anderen Fällen (b, c, d).
- Strategie 2 (4 1/2 bis 6 Jahre): eindimensionaler Vergleich. In dieser Phase registrieren die Kinder nicht nur die An- oder Abwesenheit von Saft auf jeder Seite, sondern auch die Menge des Saftes, das ist die Anzahl der Becher mit Saft. Ihre Antwortstrategie ist nicht mehr nur absolut sondern vergleichend. Sie sind erfolgreich in allen Fällen, in denen das Zählen der Saftbecher auf jeder Seite die Lösung ermöglicht (a, b im Gegensatz zu c, d), d.h. sie behaupten, jenes Gefäss schmecke mehr nach Orangensaft, in das mehr Saftbecher gegossen werden.
- Strategie 3 (7 bis 8 Jahre): zweidimensionaler Vergleich. Nun wird auch die Zahl der Wasserbecher beachtet und nicht mehr bloss die Zahl der Saftbecher. Die Strategie besteht darin, die relative Zahl der Wasser- und der Saftbecher auf jeder Seite zu berechnen und jene Seite zu wählen, bei der die Zahl der Saftbecher überwiegt. Wenn auf beiden Seiten nun aber die Zahl der Saftbecher überwiegt (d) oder wenn beide Seiten mehr Wasserbecher haben, sind die Kinder noch nicht zu einer korrekten Antwort fähig.
- Strategie 4 (9 bis 10 Jahre): zweidimensionaler Vergleich mit Quantifizierung. Im Alter von neun Jahren etwa beginnen die Kinder nicht nur die relative Zahl von Saft- und Wasserbechern zu betrachten, sondern die Proportion zu quantifizieren, so dass sie fähig sind, alle Probleme zu lösen.
Anhand dieses Beispiels wird ersichtlich, dass jede Strategie eine modifizierte und leistungsfähigere Version der vorhergehenden darstellt. All diese Strategien lösen einige Probleme und alle machen in einer gewissen Weise Sinn. Jedes höhere Niveau erlaubt die Lösung einer grösseren Zahl und Vielfalt von Problemen, da einige neue relevante Aspekte der Aufgabe zusätzlich einbezogen werden. Gemäss Piaget schliesst jede neue Strategie die Elemente der vorhergehenden ein, ist aber differenzierter und gleichgewichtiger als diese. Die Begriffe "Reversibilität" und "Beweglichkeit" der Transformationen haben in seinem Denken eine grosse Bedeutung. Er sieht die geistige Entwicklung als eine Entwicklung auf grössere Beweglichkeit des Denkens hin. Piaget sprach auch vom hypothetisch-deduktiven Denken (sog. structure ensemble), also einem in sich geschlossenen Gesamtsystem des Denkens.
Die formal-operationale Phase stellt somit das Erreichen des Entwicklungsoptimums des Denkens dar:
- Das Kind kann sich von der konkreten Ausgangssituation lösen und ist fähig, mit hypothetisch angenommenen Sachverhalten zu operieren.
- Systematisches Vorgehen ist möglich.
- Sämtliche in Betracht kommenden Erklärungen werden in Erwägung gezogen und alle Möglichkeiten vergegenwärtigt, die in einer Problemsituation enthalten sind.
- Das Kind verlässt sich auf die eigenen Schlussfolgerungen ohne dass diese durch den Augenschein beeinflusst würden.
- Das Kind zeigt zunehmend Interesse an abstrakten und theoretischen Fragen.
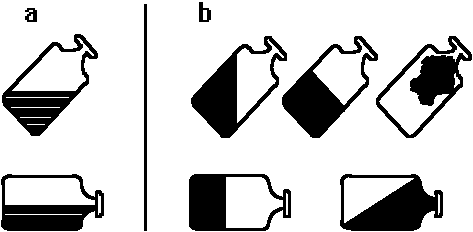
Abb.: Demonstration des Wasserspiegels in der gekippten Flasche (a) und typischer Fehler (b) der Reproduktion
Chemischer Versuch
Piaget und Inhelder legten den Versuchspersonen vier gleiche Fläschchen mit geruch-, geschmack- und farblosen Flüssigkeiten vor, die sich äußerlich in nichts voneinander unterschieden. Fläschchen I enthielt gelöste Schwefelsäure, Fläschchen 2 Wasser, Fläschchen 3 Wasserstoffsuperoxyd, Fläschchen 4 Thiosulfat. Dazu kam noch ein Gefäß mit Tropfenzähler, das Kaliumjodid enthielt (g). Bei Vermischung von 1 und 3 mit einigen Tropfen aus g färbt sich die Flüssigkeit gelb. Bei Hinzufügen von 2 ändert sich nichts, bei Zugießen von 4 verschwindet die gelbe Farbe. Der Versuchsleiter zeigte dem Kind zwei Gläser, die scheinbar die gleiche Flüssigkeit enthielten und setzte bei beiden einige Tropfen aus g hinzu. Da das eine Glas aus 1 und 3 gemischt war, färbte sich die Flüssigkeit gelb, das andere Glas, das nur Wasser enthielt, blieb farblos. Das Kind sollte das gleiche Ergebnis unter Benutzung der vier bereitgestellten Fläschchen und des Gefäßes erzielen.
Schon die Sieben- bis Zehnjährigen bemühten sich um eine systematische Lösung. Sie mischten g mit allen anderen Flüssigkeiten einzeln oder schütteten alle Flüssigkeiten zusammen. Die Lösung erfordert aber ein komplexeres Denken. Der Farbeffekt kann erst bei Verwendung formaler Operationen durch Mischung dreier Flüssigkeiten (1 + 3 + g) bei gleichzeitiger Abwesenheit der vierten (4) erzielt werden. Auf der Stufe der formalen Operationen erstellen der Jugendliche (nach anfänglichen Fehlversuchen) alle möglichen Kombinationen, auch die möglichen sechs zweier Flüssigkeiten zusammen mit g. Damit ist eine Variablenkontrolle realisiert.
Zeichnungen: http://www.stud.uni-wuppertal.de/~ya0023/hotlist.htm
inhalt :::: nachricht :::: news :::: impressum :::: datenschutz :::: autor :::: copyright :::: zitieren ::::