Sudoku lösen - Wie man sein Gedächtnis beim Lösen unterstützt
 Sudoku
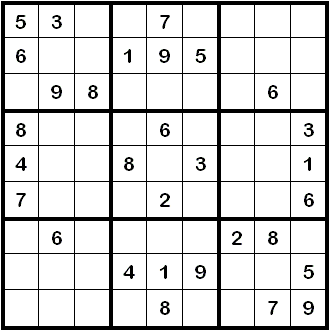
ist ein Zahlenpuzzlespiel, wobei das "Spielfeld" quadratisch und in
drei mal drei Blöcke unterteilt ist (siehe das Beispiel links). Jeder
dieser Blöcke besteht aus neun Kästchen, sodass das Gesamtquadrat also
81 Felder in 9 Reihen und 9 Spalten enthält. Typischerweise sind 22 bis
36 Felder von den 81 möglichen vorgegeben, in denen schon Zahlen von 1
bis 9 stehen.
Sudoku
ist ein Zahlenpuzzlespiel, wobei das "Spielfeld" quadratisch und in
drei mal drei Blöcke unterteilt ist (siehe das Beispiel links). Jeder
dieser Blöcke besteht aus neun Kästchen, sodass das Gesamtquadrat also
81 Felder in 9 Reihen und 9 Spalten enthält. Typischerweise sind 22 bis
36 Felder von den 81 möglichen vorgegeben, in denen schon Zahlen von 1
bis 9 stehen.
Der Spieler hat nun die Aufgabe, das Puzzle dadurch zu vervollständigen, indem er in die leeren Kästchen die richtigen Ziffern einträgt, die folgende Bedingungen erfüllen müssen: in jeder Zeile, jeder Spalte und in jedem Block dürfen die Ziffern von eins bis neun immer nur einmal vorkommen. Das Sudoku ist gelöst, wenn alle Kästchen korrekt ausgefüllt wurden.
Geschichte: Sudokus sind eine Variante der lateinischen Quadrate, wobei schon aus der Zeit des chinesischen Kaisers Lo-Shu (2200 vor Christ) ein solches magisches Quadrat dritter Ordnung überliefert ist. Der Gelehrten Manuel Moschopoulos hat der Anfang des 15. Jahrhunderts in Konstantinopel Konstruktionsregeln für magische Quadrate jeder Ordnung aufgeführt. Nach dessen Anleitungen hat dann Cornelius Agrippa von Nettesheim um 1500 magische Quadrate der Ordnungen drei bis neun entwickelt und diese den Planeten zugeordnet. Als Rätselspiel wurde es dann unter dem Namen "Lateinisches Quadrat" vom Schweizer Mathematiker Leonhard Euler im 18. Jahrhundert weiterentwickelt, das im Gegensatz zum Sudoku aber nicht in Blöcke (Unterquadrate) unterteilt ist. Das heutige Sudoku stammt aus den USA, wo es 1979 in der Zeitschrift Math Puzzels & Logic Problems erstmals publiziert wurde, und zwar von dem Architekten Howard Garns unter dem Namen "Number Place", zu deutsch "Zahlenplatz". Seinen Durchbruch erlangte das Sudoku jedoch erst um etwa 1984, als die japanische Zeitschrift Nikoli dieses zunächst unter dem Namen Suji wa dokushin ni kagiru (Japanisch: "Die Zahlen dürfen nur einmal vorkommen") regelmäßig abdruckte. Hieraus entwickelte sich schließlich der Begriff Sudoku. Der Neuseeländer Wayne Gould hat Sudoku auf einer Japanreise kennen gelernt. Sechs Jahre brauchte er, um eine Software zu entwickeln, die neue Sudokus per Knopfdruck entwickeln kann. Anschließend bot er seine Rätsel der „Times“ in London an. Die Tageszeitung druckte die ersten Sudoku-Rätsel und trat auf diese Weise eine Sudoku-Lawine in der westlichen Welt los. Inzwischen haben schätzungsweise 100 Millionen Menschen weltweit mindestens eine Partie Sudoku gespielt. Der Name "Sudoku" wurde als Marke eingetragen; mittlerweile gibt es viele verschiedene Varianten des Rätsels; 2006 wurde erstmals eine Sudoku-Weltmeisterschaft ausgetragen.
Da das  Lösen von Sudokus eine interessante Form der Konzentrationsübung darstellt bzw. in gewissem Ausmaß auch der Förderung des logischen Denkens
dient, kann es aus pädagogischer und lernpsychologischer Sicht vor
allem deshalb empfohlen werden, da es im Gegensatz zu anderen Übungen in
erster Linie nicht auf erlernte oder erlernbare Wissensinhalte abzielt,
sondern vom Prinzip her "reines" Denken fördert und schult.
Lösen von Sudokus eine interessante Form der Konzentrationsübung darstellt bzw. in gewissem Ausmaß auch der Förderung des logischen Denkens
dient, kann es aus pädagogischer und lernpsychologischer Sicht vor
allem deshalb empfohlen werden, da es im Gegensatz zu anderen Übungen in
erster Linie nicht auf erlernte oder erlernbare Wissensinhalte abzielt,
sondern vom Prinzip her "reines" Denken fördert und schult.
Als echter Denksport sind Sudokus aber nur in begrenztem Maße geeignet, denn zwar stellen diese anfangs eine gewisse Herausforderung dar, doch wird mit der Zeit ein großer Teil der Gedankenarbeit beim Lösen zur Routine, was immerhin noch die Konzentration fördert. Auch wird man beim Lösen von Sudokus immer schneller, doch das bedeutet nicht, dass man dabei noch das Gehirn trainiert. Im Rahmen von Gehirnjogging-Programmen, die Gedächtnis und Gehirnleistung trainieren sollen, erleben Sudokus derzeit einen Boom. In den USA gibt es sogar „Fitness-Studios" fürs Gehirn, in denen Menschen reihenweise vor Computern sitzen und durch das Spielen verschiedener Programme ihre Intelligenz steigern wollen. Doch es gibt kein Training, das den Menschen klüger macht, allerdings lassen sich bestimmte Gedächtnisfunktionen gut trainieren. Werden etwa Wortreihen regelmäßig auswendig gelernt, so wird der Lernende genau in diesem Bereich besser werden. Dass Sudoku-Lösen allgemein das Arbeitsgedächtnis oder die Wahrnehmungsgeschwindigkeit verbessert, ist jedoch noch nicht bestätigt, denn auch Sudoku-Lösen führt nur dazu, dass man in dieser Tätigkeit besser wird. Auch Elisabeth Stern (ETH Zürich) gesteht Sudokus nur in sehr engem Rahmen fördernde Wirkung auf das Denken zu, denn das häufige Lösen bestimmter Denksportaufgaben verbessert zwar tatsächlich die Fähigkeit, eben genau diese Aufgaben schnell und gut lösen zu können, aber dieser Trainingseffekt tritt auch bei ganz alltäglichen Aufgaben auf, denn neue synaptische Verbindungen im Gehirn entstehen immer dann, wenn sich Menschen mit etwas geistig auseinandersetzen. Sinnstiftendes Wissen entsteht aber nicht in der Wiederholung immer gleicher Schemata, sondern erst durch die geistige Auseinandersetzung mit immer neuen Ereignissen und Begriffen. Immerhin können solche Denksportaufgaben zeigen, wie Motivation zum Lernen gut funktionieren kann.
Dazu in ein einer Fernsehsendung:
"Das Gehirn ist gar nicht darauf ausgelegt, Sudokus zu lösen. Das Hirn soll Reize aus der Umwelt einordnen und interpretieren, damit man sich auch in ihr zurechtfinden kann. Das ist die ursprüngliche Aufgabe des Hirns. Genau das muss man trainieren. Das heißt, man muss an der frischen Luft sein, mit Menschen zusammen sein, was lesen, was für den Geist machen und dabei Spaß haben."
Andere Spiele wie Memory fördern daher vermutlich nicht nur die Konzentration sondern auch das bildhafte Gedächtnis, Schach stärkt das analytische und strategische Denken. Kreuzworträtsel oder Ratespiele wie Trivial Pursuit können ebenfalls eher so gestaltet werden, dass sie das Gedächtnis trainieren.
Obwohl Sudoku üblicherweise mit Ziffern gespielt werden, handelt es sich um kein mathematisches Rätsel, denn die Ziffern lassen sich auch durch Farben oder Zeichen ersetzen. Ein Grund für den seit einigen Jahren anhaltenden Erfolg ist vermutlich, dass zum Finden der Lösung ausschließlich logisches Denken erforderlich ist. "Man benötigt kein auswendig gelerntes Wissen, kein Mathematikdiplom und kein Spezialwerkzeug - ein Bleistift und eine Sitzgelegenheit reichen aus", heißt es auf einer einschlägigen Webseite.
Es empfiehlt sich, mit leichten Rätseln zu beginnen (werden in der Regel gekennzeichnet), um das Lösungsprinzip zu erlernen. In zahlreichen Tageszeitungen findet man heute diese derzeit auch ein wenig in Mode gekommene Rätselform, die in vielen Fällen diese auch im Internet zum Ausdrucken anbieten:
Um sich das Lösen zu erleichtern und um sich die notwendige Kombinatorik des Denkens bei komplexeren Rätseln zu erleichtern, empfehle ich das rechts stehende Schema für den systematischen Ausschluss von Zahlen. Dabei wird ein zusätzlicher Raster über das gesamte Sudoku gelegt, das innerhalb aller leeren Felder die Ziffern von 1 bis 9 symbolisiert - gewissermaßen wird das Feld in insgesamt 729 Hilfsfelder zerlegt. Mit Hilfe dieses Rasters können systematisch durch Ankreuzen jene Zahlen ausgeschlossen werden, die in einem Feld nicht stehen können. Denn Sudokus löst man - im Gegensatz zu den meisten anderen Rätseln - leichter durch ein Ausschlussverfahren als durch das sonst übliche Bestimmen der möglichen Zahlen.
Auch wenn Sudokus keine mathematischen Rätsel sind, so läßt sich das Problem bzw. dessen Lösung mathematisch definieren: Es handelt sich um ein Schnittmengenproblem, denn aus den jeweils vorgegebenen Ziffern lässt sich für jedes Feld die Schnittmenge dieser drei Mengen aus Zeile, Spalte und 9-er Block für das Feld bestimmen. Kommen beispielsweise in einer Zeile die Zahlen 1, 7, 4 und 9 in der Spalte 5, 4 und 8 und im Block 6 und 8 vor, so ergibt sich eine Schnittmenge von 1, 4, 5, 6, 7, 8 und 9 bzw. die Komplemente (=Ergänzung auf die Gesamtmenge) sind also 2 und 3, die in diesem Feld stehen können. Wenn das Komplement nur mehr eine Zahl zulässt, dann kann man diese sofort als Lösung eintragen, was allerdings nur bei leichten Sudokus möglich ist. Weitere Lösungen ergeben sich jedoch durch den Vergleich dieser Komplemente eines Feldes mit den Komplementen anderer Felder. In schwierigeren Sudokus müssen Paare oder Tripel von Ziffernkandidaten gleichzeitig betrachtet werden, um die Kandidatenmengen zu verkleinern. Hierbei werden logische Verknüpfungen zwischen mehreren Feldern gesucht, von denen klar ist, dass bestimmte Zahlen in den Feldern dieser Gruppe stehen, wodurch diese Zahlen für die nicht in der Gruppe befindliche als Lösungen ausscheiden. Falls jedoch keine einzige Ziffernmenge existiert, wählt man in einem Versuch-und-Irrtum-Verfahren aus einer der Mengen - sinnvollerweise beginnend bei der kleinsten - eine Zahl aus, um eine der möglichen Lösungen zu erhalten.
Bei der im Folgenden beschriebenen Negativmethode werden daher nicht mögliche Lösungen in den einzelnen Feldern gesucht, sondern die Zahlen, die in einem Feld auf keinen Fall stehen können. Man sollte dieses Schema bei den ersten Versuchen mit einem dünnen Bleistift vorzeichnen (siehe die oben stehende Grafik), allerdings entwickelt man mit der Zeit einen Blick für die neun Kreuzchenpositionen, sodass man in der Folge auch ohne diese Hilfslinien auskommt. Empfehlenswert ist auch zum Ankreuzen einen dünnen Bleistift zu verwenden, während man die gefundenen bzw. bestätigten Zahlen mit einem dickeren Stift darüber schreibt - man kann zuvor auch das Feld "frei radieren".
Die Schritte der Methode des "Negativrasters"
Nachdem man den Raster eingezeichnet hat - man kann das bei einem digital vorliegenden Sudoku auch mit Hilfe eines Grafikprogramms machen -, beginnt man systematisch mit dem Ausschluss der nicht möglichen Zahlen, wie sie durch die Aufgabenstellung vorgegeben sind.- Man beginnt am Besten zunächst Reihe für Reihe jene Ziffernfelder in den leeren Hilfskästchen anzukreuzen, die in dieser Reihe schon vorgegeben sind (im unten stehenden Beispiel der Übersicht halber blau angekreuzt - in der Praxis benötigt man diese farbliche Unterscheidung natürlich nicht!).
- Danach führt man dieses Ankreuzen auch in allen senkrechten Spalten durch (rot), wobei sich natürlich bereits Überschneidungen zeigen.
- In einem dritten Schritt muss man dann innerhalb der neun Blöcke ebenfalls noch jene Zahlen ankreuzen, die dort von Anfang an vorgegeben sind (grün) - meist sind es nur noch wenige.
Im dem unten stehenden Schema sind zur Illustration diese Ankreuzungen für die ersten drei waagrechten Reihen, die ersten drei senkrechten Spalten und den ersten Neunerblock vorgenommen worden:
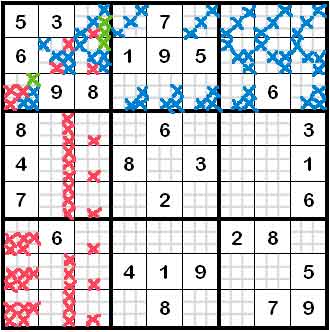
Daraus kann man erkennen, dass durch diese Methode die Komplexität des Rätsels deutlich reduziert wird bzw. bei sorgfältigem Arbeiten in der Folge auch mögliche "Denkfehler" verhindert werden. Im Prinzip erspart dieses schematische Vorgehen zwar nicht das eigentliche Denken und Kombinieren, macht es allerdings auch dem Anfänger möglich, relativ rasch das Prinzip zu erlernen und verhindert, seltener durch Fehlschlüsse entmutigt zu werden. So sieht man im obigen Beispiel, dass in der ersten Spalte unter den Feldern 5 und 6 nur mehr die Ziffern 1 oder 2 möglich sind.
Bei leichten Sudokus mit vielen Zahlenvorgaben werden schon nach diesen ersten drei systematischen Durchgängen einzelne Zahlen feststehen, die man sofort richtig eintragen kann. Dabei muss man in einem vierten Schritt die neuen Zahlen ebenso systematisch für die restlichen Felder durch Ankreuzen in den Reihen, Spalten und Neunerblöcken "eliminieren", wodurch sich in einer Art Schneeballsystem meist weitere Ziiffern bzw. Lösungen ergeben.
 Bei schwierigen Sudokus
- insbesondere bei solchen, bei denen mehrere Gabelungen
(Bifurkationen) auftreten - kommt es natürlich eher selten zu
"automatischen" Lösungen, aber die Ankreuzungen helfen einem in jedem
Fall, Fehler zu vermeiden. Theoretisch erfordern Gabelungen ein
Vorausdenken von oft mehr als zehn Lösungsschritten, wodurch auch manche
"Experten" überfordert sind, sodass auch diese dann ein systematisches
Probieren anwenden (Backtracking, Trial and Error). Hier hilft es, zwei
oder mehr Kopien des jeweiligen Spielstandes anzufertigen, und diese
Gabelungen der Reihe nach systematisch weiter zu führen, bis das Rätsel
gelöst ist oder man erkennt, dass der andere Weg einzuschlagen gewesen
wäre.
Bei schwierigen Sudokus
- insbesondere bei solchen, bei denen mehrere Gabelungen
(Bifurkationen) auftreten - kommt es natürlich eher selten zu
"automatischen" Lösungen, aber die Ankreuzungen helfen einem in jedem
Fall, Fehler zu vermeiden. Theoretisch erfordern Gabelungen ein
Vorausdenken von oft mehr als zehn Lösungsschritten, wodurch auch manche
"Experten" überfordert sind, sodass auch diese dann ein systematisches
Probieren anwenden (Backtracking, Trial and Error). Hier hilft es, zwei
oder mehr Kopien des jeweiligen Spielstandes anzufertigen, und diese
Gabelungen der Reihe nach systematisch weiter zu führen, bis das Rätsel
gelöst ist oder man erkennt, dass der andere Weg einzuschlagen gewesen
wäre.
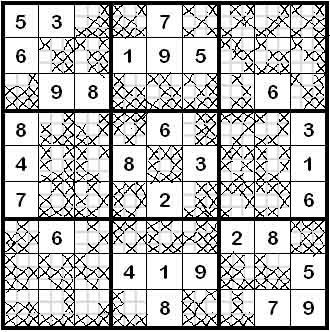
Beispiel der Negativmethode: Die ersten drei Schritte der Negativmethode wurden im links stehenden Schema exemplarisch durchgeführt. Schon diese systematische Reduktion ergibt z.B. eine erste einsetzbare Zahl (4) im neunten Block. Im mittleren Block ergibt sich die 5, aus der sich in der Folge die mittlere Spalte sofort vervollständigen lässt, da sich aus dem Einsetzen der 5 die Position der 3 und der 4 ebenso ergibt. Natürlich muss man bei jeder eingesetzten Zahl die ersten drei Schritte ebenfalls durchführen, wobei sich bei leichten und auch mittelschweren Rätseln weitere Lösungen zeigen.
In der einschlägigen Literatur wird oft das Scannen nach positiven Möglichkeiten empfohlen, bei dem man z.B. die möglichen Zahlen als kleine Ziffern in die Felder eintragen kann - meist als PMs (Page Marks) bezeichnet -, allerdings verwirren diese zusätzlichen Zahlen im Rätselschema häufig den Anfänger. Da sich die "Negativmethode" nicht am symbolischen Zahlenwert sondern eher am abstrakten Zahlenraum orientiert, der allmählich für jedes Feld reduziert wird, fördert sie auch ein eher "(be)greifbares" Erleben. Es können durch diese Methode die komplexen Beziehungen zwischen den drei Grundebenen (Zeilen, Spalten, Blöcke) sowohl leichter erkannt als auch in einer angemessenen Form notiert werden. Man sollte sich übrigens nicht durch die von "ExpertInnen" oft geäußerte Kritik an der Verwendung von PMs aller Art irritieren lassen, da sie das Denken nicht ersetzen sondern unterstützen. Solche Methoden unterstützen das Erlernen und führen dazu, die Prinzipien des Sudoku später "automatisch" zu erkennen, sodass bei einfachen Rätseln auf diese Hilfsmittel wieder verzichtet werden kann.
Insbesondere ermöglich die hier vorgeschlagene Lösungsmethode, der Reihe nach jene teilweise recht komplexen Schlussfolgerungen zu erlernen, die zum Lösen schwieriger Sudokus notwendig sind. Der Reiz von Sudokus liegt nämlich nicht nur im Lösen von einzelnen Rätseln, sondern auch und im Besonderen im Gewahrwerden der durch ein plötzliches Aha-Erlebnis begleitenden Lösungsprinzipen bzw. Regeln. Daher werden diese Regeln hier auch nicht verraten, zumal sie ohnehin im Internet auf zahlreichen Seiten dargestellt sind.
Hartmut Rehlich (Fakultät für Mathematik und Informatik der FSU Jena, Abteilung Didaktik) hat innerhalb des Hamburger Modells zur Begabtenförderung
(für Mathematik) längere Zeit "an dem und um das Rätsel herum"
gearbeitet und neben den Lösungsstrategien an Bezügen zu
kombinatorischen und algebraischen Fragen gearbeitet (z.B: ist jedes
Mini-Sudoku formgleich zu einer Gruppentafel der Klein'schen
Vierergruppe oder zur Restklassengruppe modulo 4). Informationen zu
diesem Projekt finden sich unter den folgenden URLs:
http://www1.uni-hamburg.de/psych-2/EP/begabung/wilstern.html
http://www.math.uni-hamburg.de/math/mathges/veranst/Zusamm/Progr191105Sudoku1.html
Es zeigte sich, dass die hier vorgestellte Methode zur Komplexitätsreduktion durch kleine Ratefelder
in der Tat bei den Teilnehmern den Kopf für die Suche nach
"hintergründigeren Strukturen" freigemacht hat. Um diese Arbeit
zusätzlich zu beflügeln hat Hartmut Rehlich für die Teilnehmer ein Computerprogramm
entwickelt, das vielfältige Ratefelderoperationen (wie stufenloses Ein-
und Ausblenden, das Ausradieren einzelner Felder, die Durchforstung
nach subtileren Mustern und vielfältige Markieroptionen) gestattet. Es
unterscheidet sich von "kommerziellen Produkten" durch eine starke
Orientierung an heuristischen Gesichtspunkten (der Nutzer soll
schließlich eigene Entdeckungen machen). Das Skript und das Programm
finden kann unter dem URL
http://www.minet.uni-jena.de/~hrehlich/Programme/INDEX.HTM
(Persönliche Mitteilung vom 24. Oktober 2006)
Die Methode des Negativrasters wird auch auf der Seite http://www.sudoku-aktuell.de/sudoku-regeln.html als eine gute Lösungsmöglichkeit erwähnt. Auf dieser Seite kann man übrigens jeden Tag 24 Sudokus unterschiedlicher Schwierigkeitsgrade ausdrucken.
Aus motivationspsychologischer Sicht hat diese Methode darüber hinaus den Vorteil, von Anfang an sichtbare Resultate der Rätselarbeit zu erzeugen, die den Fortschritt erlebbar machen. Im Unterschied zu anderen Notationsmethoden beim Scannen der Möglichkeiten werden keine externen Hilfsmittel (zusätzliches Papier wie Notizzettel oder gar Lösungsschemata) benötigt, sondern es wird direkt im vorgegebenen Rätsel gearbeitet.
Wie andere Rätsel auch können Sudokus süchtig (Nicht substanzgebundene Drogen) machen und den durchaus positiven Aspekt, Konzentration und logisches Denken zu fördern, wieder zunichte machen.
Um nicht an einem Sudoku zu verzweifeln und eine schlaflose Nacht mit Raten und Radieren zu verbringen, bieten die meisten Anbieter von Sudoku (s.o.) entweder die Lösungen oder interaktive Rätselfelder an. Für Rätsel ohne solche Hilfsmittel hier der Hinweis auf eine Webseite, auf der man durch Eingabe der Ausgangszahlen mit einem einfachen Klick von der Ungewissheit befreit wird, dass es doch eine Lösung gib, an die man nicht mehr geglaubt hat: http://sudoku.nanosim.net/
Grundsätzliche Anmerkungen zu Markierungs- und Lösungsmethodiken
 Es
gibt mehrere Techniken, ein Sudoku zu lösen: zwei auch mit der Hand
durchführbare, die "normale Methode" und das "Negativraster", und zwei
praktischer Weise nur mit Rechenmaschinen bewältigbare, die
"Schnittmengen-Methode" und die "Backtracking-Methode".
Es
gibt mehrere Techniken, ein Sudoku zu lösen: zwei auch mit der Hand
durchführbare, die "normale Methode" und das "Negativraster", und zwei
praktischer Weise nur mit Rechenmaschinen bewältigbare, die
"Schnittmengen-Methode" und die "Backtracking-Methode".
Bei den ersten beiden Techniken häuft man alle möglichen, für ein Feld relevanten Informationen an, um so den Wert des Feldes zu bestimmen. Bei der normalen Methode markiert man für jede Zelle alle möglichen Ziffern. Am Ende der Prozedur betrachtet man jede Region im Einzelnen. Wenn eine bestimmte Ziffer innerhalb dieser Region nur ein einziges Mal in sämtlichen Möglichkeiten der freien Zellen auftaucht, so muss diese Zelle die besagte Ziffer beinhalten, unabhängig davon, welche anderen Möglichkeiten noch in der betreffenden Zelle vermerkt sind. Das von uns präferierte Negativraster funktioniert genau anders herum: es werden alle Möglichkeiten notiert, die für eine Zelle nicht in Frage kommen; die letzte noch fehlende Möglichkeit entspricht dem Wert der Zelle.
Die Lösungsstrategie mit Hilfe der Schnittmengen, ist die rechnerisch aufwändigste und komplexeste. Auch hier haben sich zwei Techniken herausgebildet, die Eliminierung und die „Was-wäre-wenn“-Methode. Die Eliminierung zielt darauf ab, aus einer Anzahl von Zellen Schritt für Schritt so viele Möglichkeiten zu entfernen, dass für jede Zelle die Anzahl von Möglichkeiten minimiert wird. Wenn nur noch eine Möglichkeit für jede Zelle existiert, muss dies die Lösung für das Rätsel sein. Dazu überprüft man, ob die Anzahl der noch offenen Ziffern für eine Reihe, Spalte oder Region gleich der Anzahl der noch offenen Zellen ist. Zwei Zellen einer Reihe, Spalte oder Region können dementsprechend nur die zwei noch offenen Möglichkeiten für diese Reihe, Spalte oder Region enthalten. Alle anderen Möglichkeiten können aus diesen Zellen eliminiert werden. Die "Was-wäre-wenn“-Methode hingegen nimmt für eine Zelle mit nur zwei Kandidaten eine der gültigen Möglichkeiten als gegeben an und das Rätsel wird auf der Grundlage dieser ersten Annahme gelöst. Sollte sich ein Widerspruch ergeben, geht man direkt zu dieser Zelle zurück und benutzt die andere Möglichkeit. Viele Logiker betrachten diese Methode jedoch als bloßes Herumprobieren und vermeiden die Verwendung, obwohl sie oft zu einem schnellen Ergebnis führen kann.
Eine letzte Strategie, die bei einem gültigen Rätsel in jedem Fall zu einem Ergebnis führt, ist die Backtracking-Methode, die aber nur mit sehr viel Geduld und Ausdauer oder mit Hilfe eines Computers benutzt werden kann. Man beginnt bei der ersten freien Zelle oben links und trägt die niedrigste Ziffer ein. Dann überprüft man die Gültigkeit dieser Ziffer anhand der vorgegebenen Zellen. Sollte sich kein Widerspruch finden lassen, wird dasselbe Prinzip mit der nächsten Zelle in der Zeile oder Spalte wiederholt. Wenn ein Widerspruch gefunden wird, wird die eingetragene Ziffer durch die nächsthöhere ersetzt. Sollte die Ziffer bereits die höchstmögliche für diese Zelle gewesen sein, geht man zur Zelle davor zurück und erhöht die Ziffer dort nach demselben Prinzip.
Quellen: Käckenmeister, Thomas & Haby, Jan Christoph (2006). Das Sudoku-Experiment. Hausarbeit. Universität Rostock: Institut für Pädagogische Psychologie Rosa und David Katz.
Das Sudoku mit Smiley stammt von "GreenSmilies - Die Welt der Smilies ist nicht immer nur gelb!" http://www.greensmilies.com/ (08-04-11)
Sudokus im Internet
Es gibt im Internet immer mehr Seiten, auf denen Sudokus in allen Varianten angeboten werden. Auf sudokuspielen.de findet sich neben der Originalvariante in verschiedenen Schwierigkeitsstufen zahlreiche Sudoku-Varianten wie Lightforce Sudoku, das Kakuro Master, das Life Sudoku, das Jigsaw Sudoku, das Samurai Sudoku sowie das Sudoku Tetris. Zahlreiche Sudokus bietet auch sudoku-knacker.de in allen Schwierigkeitsgraden. Die Site sudoku-aktuell.de bietet hundertzwanzig Spielvarianten pro Tag und ein großes Rätsel-Archiv im pdf-Format. Weitere Webangebote sind sudoku-drucken.de, sudoku-space.de, sudoku-zu-drucken.de oder sudokugarten.de.
Übrigens: Versuchen Sie nie, ein Sudoku in Anwesenheit einer schönen Frau zu lösen ;-)
Forscher der Universität Valencia ließ 84 junge Männer in Anwesenheit eines fremden Mannes und einer sehr attraktiven Frau Sudokus
lösen. Ließ die Frau die Männer kurz allein, änderte sich der Spiegel
des Stresshormons Cortisol im Blut der Testperson nicht. Verließ der
fremde Mann den Raum, schnellte der Cortisolspiegel des Probanden hoch,
denn nun war er mit der Schönen allein.
Quelle: http://www.welt.de/die-welt/wissen/article8613517/Schoene-Frauen-stressen.html (10-07-25)
Optimisten sind Menschen, die ein Sukodu mit Kugelschreiber lösen.
Einige Sudokus des Tages
Sudoku by Sudokuhints.com
[Zur Verfügung gestellt von Astraware Limited]
An manchen Tagen gibt es leider Ausfälle bei diesen Gratisangeboten. Wir bitten, etwaige Ausfälle zu entschuldigen und auf eines der oben genannten Angebote zurückzugreifen.
Quellen: Das als Beispiel verwendete Sudoku stammt wie die Kurzbeschreibung des Systems aus Wikipedia: http://de.wikipedia.org/wiki/Sudoku. Die Sudoku des Tages stammen aus dem Angebot von http://www.sudokuhints.com/, https://www.sudokuoftheday.com/ und https://www.sudokufun.com/
inhalt :::: nachricht :::: news :::: impressum :::: datenschutz :::: autor :::: copyright :::: zitieren ::::